Encontrar el mínimo en una ecuación por aproximaciones

El perceptrón simple que hemos visto en Perceptrón básico con funciones AND y OR tiene el límite de que sólo sirve cuando la solución se puede separar con una recta.

En cambio, el perceptrón simple no sirve si se quiere abordar un problema que requiera dos separaciones, como por ejemplo la tabla XOR. Entonces se necesitan varias neuronas puestas en capas. Esto implica varios pesos, y el reto es cómo dar con el peso correcto para cada valor (en la mencionada entrada ya vimos cómo buscarlos de manera aleatoria y con la fórmula de Frank Rosenblatt).

Una base matemática que ayuda a deducir los pesos en este tipo de red neuronal es el cálculo del mínimo de una ecuación, esto es, el valor de x para el valor mínimo de y.

Para obtenerlo a continuación se implementa con Dart un método que, a partir de un valor arbitario de x en una ecuación de 2º grado tipo ax² + bx + c, utiliza aproximaciones sucesivas para obtener el valor mínimo de y.

import 'dart:io';

const dec = 3; // número de decimales en resultados

void main() {
  // valores de la ecuación
  double a;
  double b;
  double c;
  double x;

  // pide los valores de la ecuación y el valor inicial de x
  print('Siendo la ecuación ax² + bx + c');
  stdout.write('Introduce el valor de a (un número mayor que 0, por defecto 5.0): ');
  a = double.tryParse(stdin.readLineSync()) ?? 5.0;
  a = a <= 0.0 ? 5.0 : a;
  stdout.write('Introduce el valor de b (por defecto -7.0): ');
  b = double.tryParse(stdin.readLineSync()) ?? -7.0;
  stdout.write('Introduce el valor de c (por defecto -13.0): ');
  c = double.tryParse(stdin.readLineSync()) ?? -13.0;
  stdout.write('Introduce el valor inicial de x (por defecto 1.0): ');
  x = double.tryParse(stdin.readLineSync()) ?? 1.0;

  // calcula y muestra el valor inicial de y
  double ecuacion(double x) => a * x * x + b * x + c;
  var yIni = ecuacion(x);
  var cont = 1;
  print('$cont x: ${x.toStringAsFixed(dec)} y: ${yIni.toStringAsFixed(dec)}');

  // método por aproximaciones
  var variacion = 1.0; // variación inicial de x
  while (variacion.abs() > 0.00001) {
    var yNew = ecuacion(x + variacion); // se aplica la variación a x
    if (yNew > yIni) {
      variacion = (-1 * variacion) / 10; // se reajusta la variación de x
    } else {
      yIni = yNew; // se acepta el nuevo valor de Y
      x += variacion; // nuevo valor de X
      cont++;
      print('$cont x: ${x.toStringAsFixed(dec)} y: ${yIni.toStringAsFixed(dec)}');
    }
  }

  // mostrar ecuación y resultado
  String sinCeros(numero) => numero.toString().replaceAll(RegExp(r'([.]*0)(?!.*\d)'), '');
  String signo(numero) => numero < 0 ? '-' : '+';
  print('En la ecuación y = ${sinCeros(a)}x² ${signo(b)} ${sinCeros(b.abs())}x ${signo(c)} ${sinCeros(c.abs())}');
  print('para el valor mínimo de y = ${yIni.toStringAsFixed(dec)}, x = ${x.toStringAsFixed(dec)}');
}

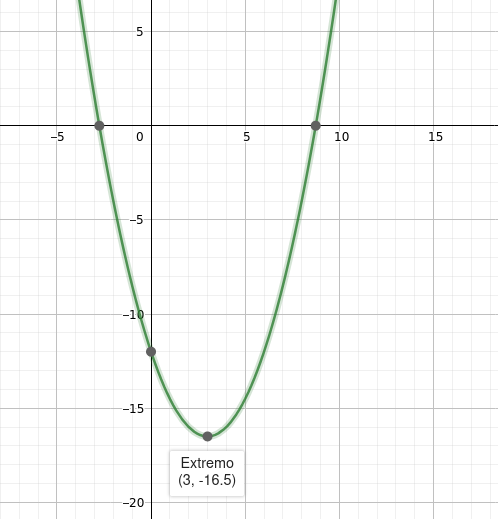
Al ejecutar el código se pueden ajustar los valores de la ecuación y del valor inicial de x. Ésta es la salida en consola introduciendo la siguiente ecuación con un valor inicial de -0.5 (la curva resultante aparece en la imagen superior):

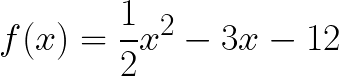
Siendo la ecuación ax² + bx + c
Introduce el valor de a (un número distinto de 0, por defecto 5.0): 0.5
Introduce el valor de b (por defecto -7.0): -3
Introduce el valor de c (por defecto -13.0): -12
Introduce el valor inicial de x (por defecto 1.0): -0.5
1 x: -0.500 y: -10.375
2 x: 0.500 y: -13.375
3 x: 1.500 y: -15.375
4 x: 2.500 y: -16.375
5 x: 3.500 y: -16.375
6 x: 3.400 y: -16.420
7 x: 3.300 y: -16.455
8 x: 3.200 y: -16.480
9 x: 3.100 y: -16.495
10 x: 3.000 y: -16.500
En la ecuación y = 0.5x² - 3x - 12
para el valor mínimo de y = -16.500, x = 3.000
Process finished with exit code 0

Por supuesto, tal como está escrito, este método por aproximaciones solo es válido cuando la curva en el gráfico está orientada hacia arriba, esto es, cuando la constante a tiene un valor positivo (por eso el código no admite valores inferiores a 0 para a) puesto que en caso contrario habría que hallar el máximo y no el mínimo, pero sirve como una primera aproximación al cálculo de los pesos en redes neuronales complejas.