Perceptrón básico con funciones AND y OR
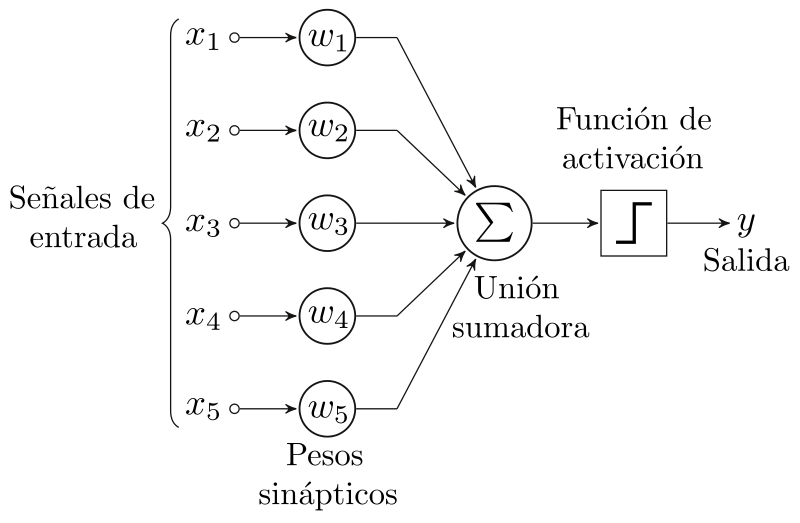
Diagrama de un perceptron con cinco señales de entrada (Alejandro Cartas / CC BY-SA).
Ejercicio de implementación con Dart de red neuronal básica para aprendizaje de funciones lógicas AND y OR utilizando la fórmula de Frank Rosenblatt.
Las funciones lógicas de conjunción (AND) y disyunción (OR) se comportan según la siguiente tabla de verdad con dos señales de entrada:
INPUT OUT A B | AND | OR --- --- |-----|----- 1 1 | 1 | 1 1 0 | 0 | 1 0 1 | 0 | 1 0 0 | 0 | 0
Algoritmo que implementa una unidad básica (perceptrón simple) que toma dos señales de entrada (A y B) y una salida (S):
- Se calcula la suma de los valores con sus pesos más el peso de umbral constante (1):
valor = (A1 * P1) + (A2 * P2) + (1 * PU)
- Se obtiene el valor de salida en función de ese valor:
S = f ( valor ) : si valor > 0 -> S = 1 (else S = 0)
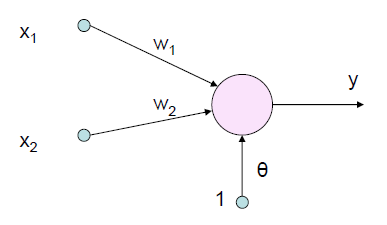
Estructura de una neurona de McCulloch-Pitts para solución de funciones lógicas.
Para aplicar la función AND o la función OR en el siguiente código solo hay que cambiar la tabla de datos que sirven para aprender (lo que se hace comentando y descompentando la variable tabla correspondiente a cada función). En el bucle de aprendizaje se ve comentado un método de búsqueda aleatoria de nuevos pesos, que aunque funciona ha sido sustituido por la fórmula de Frank Rosenblatt, la cual utiliza una tasa de aprendizaje (un valor entre 0 y 1) para buscar los nuevos pesos.
// Redes neuronales: perceptrón básico con funciones AND y OR
import 'dart:math';
void main() {
// devuelve valor double entre -1 y +1 para generar pesos aleatorios
double _random() {
var random = Random();
var positivo = random.nextBool();
var randomDouble = random.nextDouble();
return positivo ? randomDouble : -1 * randomDouble;
}
// tabla de verdad de la función AND
var tabla = [
[1, 1, 1],
[1, 0, 0],
[0, 1, 0],
[0, 0, 0]
];
// tabla de verdad de la función OR
/* var tabla = [
[1, 1, 1],
[1, 0, 1],
[0, 1, 1],
[0, 0, 0]
]; */
var pesos = List.generate(3, (int index) => _random());
int salida;
var iteraciones = 0;
var tasaAprende = 0.3;
// proceso de aprendizaje
var aprendiendo = true;
while (aprendiendo) {
aprendiendo = false;
iteraciones++;
for (var indexInput = 0; indexInput < tabla.length; indexInput++) {
var valor = (tabla[indexInput][0] * pesos[0]) +
(tabla[indexInput][1] * pesos[1]) +
pesos[2];
salida = valor > 0 ? 1 : 0;
/* busca nuevos pesos aleatorios
if (salida != tabla[i][2]) {
for (var i = 0; i < pesos.length; i++) {
pesos[i] = _random();
}
aprendiendo = true;
} */
var error = tabla[indexInput][2] - salida;
if (error != 0) {
for (var indexPeso = 0; indexPeso < pesos.length; indexPeso++) {
var valorInput = indexPeso == 2 ? 1 : tabla[indexInput][indexPeso];
// busca pesos con la fórmula de Frank Rosenblatt
pesos[indexPeso] = pesos[indexPeso] + tasaAprende * error * valorInput;
}
aprendiendo = true;
}
}
}
// muestra resultados
print('Resultados después de $iteraciones iteraciones');
for (var i = 0; i < pesos.length; i++) {
print('Peso ${i + 1}: ${pesos[i]}');
}
var resultado = 0;
print('Entradas\tEsperado\tResultado');
print('-' * 41);
for (var i = 0; i < tabla.length; i++) {
var valor =
(tabla[i][0] * pesos[0]) + (tabla[i][1] * pesos[1]) + pesos[2];
salida = valor > 0 ? 1 : 0;
print(' ${tabla[i][0]} y ${tabla[i][1]}'
'\t\t ${tabla[i][2]}'
'\t\t $salida');
if (salida == tabla[i][2]) resultado++;
}
print('PERCEPTRÓN ${(resultado * 100) ~/ 4}% OK');
}
Algunas salidas:
Resultados después de 9 iteraciones
Peso 1: 0.14611418985975438
Peso 2: 0.5816195930359603
Peso 3: -0.6645050996430357
Entradas Esperado Resultado
-----------------------------------------
1 y 1 1 1
1 y 0 0 0
0 y 1 0 0
0 y 0 0 0
PERCEPTRÓN 100% OK
Resultados después de 4 iteraciones
Peso 1: 0.2844389527649815
Peso 2: 0.37329602079171315
Peso 3: -0.6299447683219594
Entradas Esperado Resultado
-----------------------------------------
1 y 1 1 1
1 y 0 0 0
0 y 1 0 0
0 y 0 0 0
PERCEPTRÓN 100% OK