Resolver rompecabezas de manera casi inteligente
Ejercicio de programación con Dart a partir de la entrada Razonando como un niño del blog Divertimentos informáticos (parece que el blog no siempre está disponible pero hay una recopilación en Divertimentos Informáticos for Newbies).
La tarea consiste en resolver un rompecabezas en serie (piezas 1, 2, 3 y 4) ordenando las piezas de una manera suficientemente eficiente.
Siguiendo los principios del texto original se han limitado las acciones posibles a intercambios entre las piezas contigüas, aunque si se añadiera la posibilidad de intercambio entre piezas no contigüas se aumentaría la eficiencia.
La lógica emplea un árbol de posibilidades que se va expandiendo o ramificando según se van probando posibles soluciones que son el resultado de aplicar sistemáticamente los intercambios entre las piezas. Si no se encuentra la solución en el primer nodo, se explora y recorre un nuevo nivel o nodo.
Para mejorar la eficiencia (y aumentar la inteligencia al evitar movimientos tontos) se descartan, entre otras, las soluciones propuestas que empeoran el estado previo (así, se descarta expandir un nuevo nodo o rama a partir de esa mala solución). Se trata de explorar solo las propuestas que se acercan a la solución y descartar el resto (queremos ser más inteligentes que sistemáticos). Posiblemente se pueden mejorar o añadir los criterios de calidad de cada posible solución.
Como en el código del texto de origen (con python), se utiliza una función recursiva, aunque se ha prescindido de usar una clase. Ésta es mi primera aproximación a este tipo de ejercicios, por lo que seguro es muy mejorable. El código está comentado para facilitar su comprensión.
void main() {
var estado_inicial = [4, 2, 3, 1];
var estado_solucion = [1, 2, 3, 4];
var estado_temporal = <int>[];
var listaEstados = <List<int>>[];
var movimientos = 0;
var nodo = 0;
var solucionado = false;
// compara estados
bool equalEstados(List<int> list1, List<int> list2) {
if (list1.length != list2.length) return false;
for (var i = 0; i < list1.length; i++) {
if (list1[i] != list2[i]) return false;
}
return true;
}
void buscarSolucion() {
bool checkCalidad(List<int> estado1, List<int> estado2) {
var calidad1 = 0;
var calidad2 = 0;
for (var i = 0; i < 3; i++) {
if (estado1[i] < estado1[i + 1]) {
calidad1++;
}
if (estado2[i] < estado2[i + 1]) {
calidad2++;
}
}
return calidad2 >= calidad1;
}
void moverPiezas(List<int> estado, int pos1, int pos2) {
movimientos++;
estado_temporal = List.from(estado); //[]..addAll(estado);
if (estado_temporal[pos1] != estado_solucion[pos1]) {
//si la pieza 1 está en su lugar no la cambia
estado_temporal[pos1] = estado[pos2];
estado_temporal[pos2] = estado[pos1];
}
// se considera la solución temporal
// si es mejor que la solución de su nodo padre
// y si no está repetida
// y si no es el estado de inicio
if (checkCalidad(estado, estado_temporal) &&
!listaEstados.any((ls) => equalEstados(estado_temporal, ls)) &&
!equalEstados(estado_temporal, estado_inicial)) {
listaEstados.add(List.from(estado_temporal));
}
if (equalEstados(estado_temporal, estado_solucion)) {
solucionado = true;
} else if (movimientos < 3) {
// máximo numero de movimientos contigüos para cada estado temporal
// pendiente añadir movimientos no contigüos: 1-3, 1-4 y 2-4
moverPiezas(estado, pos1 + 1, pos2 + 1);
} else {
// cuando ha realizado todos los movimientos posibles, desciende un nivel
movimientos = 0;
nodo++;
if (nodo <= listaEstados.length) {
moverPiezas(listaEstados[nodo - 1], 0, 1);
}
}
}
moverPiezas(estado_inicial, 0, 1);
}
// inicio
print('0 $estado_inicial');
if (equalEstados(estado_inicial, estado_solucion)) {
print('NADA QUE HACER');
} else {
buscarSolucion();
}
// mostrar resultados
for (var i = 0; i < listaEstados.length; i++) {
print('${i + 1} ${listaEstados[i]}');
}
print(
'Solución $solucionado con ${listaEstados.length} movimientos en ${nodo + 1} nodos');
}
0 [4, 2, 3, 1]
1 [2, 4, 3, 1]
2 [2, 3, 4, 1]
3 [2, 3, 1, 4]
4 [2, 1, 3, 4]
5 [1, 2, 3, 4]
Solución true con 5 movimientos en 5 nodos
A continuación la imagen del árbol de decisiones del ejemplo. En rojo los estados descartados.
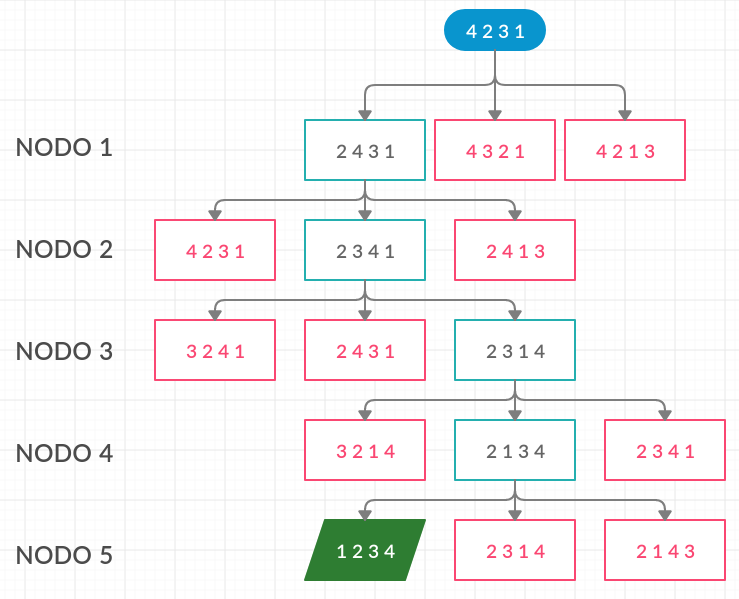
VERSIÓN MEJORADA:
Parece que funciona, pero no es lo suficientemente listo. Si queremos hacerlo semejante al razonamiento humano, hay que tener en cuenta que cuando una persona realiza esta tarea y se encuentra dos piezas correctamente posicionadas, primero, ésas ya nos las mueve, y después cambia las otras dos, con lo que soluciona el rompecabezas más rápidamente. Esto supone añadirle a la máquina la posibilidad de realizar intercambios entre piezas no contigüas. De esta manera la hacemos más inteligente y menos sistemática (no hace falta contemplar todas las opciones).
Para implementar esto, hace falta comprobar antes de cada intercambio de piezas si existen dos que ya están bien colocadas (o lo es que lo mismo, solo dos mal colocadas). Aunque esta solución sigue sin contemplar intercambios no contigüos en otras situaciones, supone una mejora considerable. El código queda así (con el mismo estado de inicio):
void main() {
var estado_inicial = [4, 2, 3, 1];
var estado_solucion = [1, 2, 3, 4];
var estado_temporal = <int>[];
var listaEstados = <List<int>>[];
var movimientos = 0;
var nodo = 0;
var solucionado = false;
var posicionesMal = <int>[];
// compara estados
bool equalEstados(List<int> list1, List<int> list2) {
if (list1.length != list2.length) return false;
for (var i = 0; i < list1.length; i++) {
if (list1[i] != list2[i]) return false;
}
return true;
}
void buscarSolucion() {
bool checkCalidad(List<int> estado1, List<int> estado2) {
var calidad1 = 0;
var calidad2 = 0;
for (var i = 0; i < 3; i++) {
if (estado1[i] < estado1[i + 1]) {
calidad1++;
}
if (estado2[i] < estado2[i + 1]) {
calidad2++;
}
}
return calidad2 >= calidad1;
}
void moverPiezas(List<int> estado, int pos1, int pos2) {
movimientos++;
estado_temporal = List.from(estado); //[]..addAll(estado);
// intercambios no contigüos
posicionesMal.clear();
for (var i = 0; i < estado_temporal.length; i++) {
if (estado_temporal[i] != estado_solucion[i]) {
posicionesMal.add(i);
}
}
if (posicionesMal.length == 2) {
estado_temporal[posicionesMal[0]] = estado[posicionesMal[1]];
estado_temporal[posicionesMal[1]] = estado[posicionesMal[0]];
} else if (estado_temporal[pos1] != estado_solucion[pos1]) {
//si la pieza 1 está en su lugar no la cambia
estado_temporal[pos1] = estado[pos2];
estado_temporal[pos2] = estado[pos1];
}
// se considera la solución temporal
// si es mejor que la solución de su nodo padre
// y si no está repetida
// y si no es el estado de inicio
if (checkCalidad(estado, estado_temporal) &&
!listaEstados.any((ls) => equalEstados(estado_temporal, ls)) &&
!equalEstados(estado_temporal, estado_inicial)) {
listaEstados.add(List.from(estado_temporal));
}
if (equalEstados(estado_temporal, estado_solucion)) {
solucionado = true;
} else if (movimientos < 3) {
// máximo numero de movimientos contigüos para cada estado temporal
moverPiezas(estado, pos1 + 1, pos2 + 1);
} else {
// cuando ha realizado todos los movimientos posibles, desciende un nivel
movimientos = 0;
nodo++;
if (nodo <= listaEstados.length) {
moverPiezas(listaEstados[nodo - 1], 0, 1);
}
}
}
moverPiezas(estado_inicial, 0, 1);
}
// inicio
print('0 $estado_inicial');
if (equalEstados(estado_inicial, estado_solucion)) {
print('NADA QUE HACER');
} else {
buscarSolucion();
}
// mostrar resultados
for (var i = 0; i < listaEstados.length; i++) {
print('${i + 1} ${listaEstados[i]}');
}
print(
'Solución $solucionado con ${listaEstados.length} movimientos en ${nodo + 1} nodos');
}
0 [4, 2, 3, 1]
1 [1, 2, 3, 4]
Solución true con 1 movimientos en 1 nodos